Math I like
2023-12-20
As documented on this site and my CV, I formally studied Math. My original plan in college was to study Math and some sort of Bio degree in hopes of going into medicine. However, after working in EMS for a little bit, and going through some of the Chemistry courses I learned it was not for me. I would learn in about my third year at Berkeley that lab sciences were my worst enemy. So I ended up sticking with Math because I was good at it and Math is in everything with crossover in all science.
My favorite Math (Fourier Analysis):
When you are studying Math, it typically breaks down into 2 different routes of study: you have more quantitative Math that concerns with explaining, or proving out some sort of physical phenomenon, and then you have Analysis-proof based Math. Personally, I like the former much better; despite the "analysis" in Fourier Analysis, it's a much more tactile subject that concerns itself with rewriting functions, (even discontinuous ones), as a sum of trigonometric functions. Hence, the "Fourier Transform". Below is a snippet from my textbook:

Of course, there's a lot of analysis that goes into proving this. With that being said, I do find it interesting and non-trivial that when taking a function that has an arbitrary point of discontinuity, transforming the function still works. In the transformation the point of discontinuity essentially can be expressed as a Fourier expansion of the function's derivative as it approaches the point.
It's just a cool thing to point out. In that class I learned a lot of cool things; pretty much anything to do with signals in the real world uses Fourier Analysis. The example we did in class was how noise cancelling headphones work, but in principal it shares core concepts in lots of things like radios, TV, 5G etc...
My least favorite (Complex Analysis)
Math 185, my worst performance in a math class at Berkeley. I thought it was a very complex class.
Complex Analysis is a continuation of Real Analysis, which I did well in. However, the difference between the two is that Real Analysis is analysis of the real number line. So most people take Calculus at some point so we're all familiar with the derivative, integrals and limits. So, how do we know things like that the real number line is continuous but uncountable given any two arbitrary bounds? Or, how do we know something converges? Real Analysis is just proving the concepts behind calculus and how they work.
Whereas Complex Analysis is the complex plane, or imaginary numbers, anything of the form a+bi. Where a and b are real components. One way to visualize what this means is look at this polar form where "a" is the length and bi describes an angle theta in relation to the imaginary plane. This is the basic, basic, level of complex numbers, the course itself gets into the calculus of the complex plane which is mainly holomorphic functions. Functions that are infinitely differentiable on a plane that "kinda" like the Cartesian coordinate system but with more endowed structures that come with complex numbers.
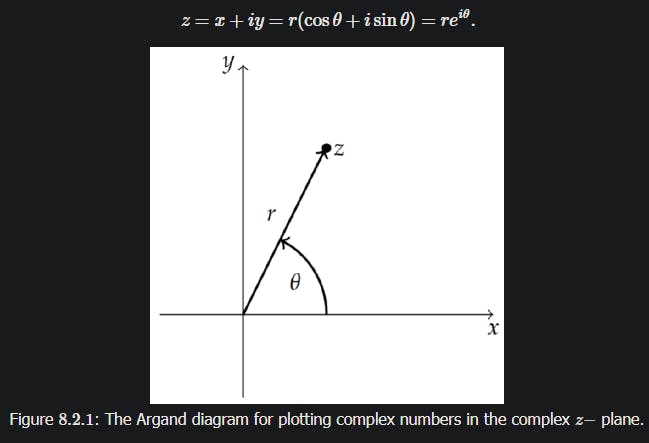
Why I don't like it
Simply put, it was hard for me to wrap my head around a lot of the ideas. At the end of the day, the way I see the complex number plane is just a very abstract way to explain distance and position/magnitude. When we discuss distance in the complex number field there is this sort of symmetry that occurs when we're able to describe points and distance with angles and arbitrary lengths. This is further abstracted to many levels when we're talking about analytical functions and ideas like the Residue Theorem. Which, speaking about lines, the Residue Theorem basically gives a way to evaluate line integrals over analytical functions (or infinitely differentiable functions in the complex plane). It's just confusing to me because this is an idea that could be applied to real line integrals which do not posses the same structure as complex integrals and do not have the same conception of integrability or differentiability. It was just a very difficult class for me, I was always in office hours and it being the height of COVID did not make it any easier.
